Recently, I was trying to figure out a way to create my own arbitrary precision floating point arithmetic library. For those of you unaware, floating point simply means numbers are represented in scientific notation and that allows computers to express really large or really small numbers and everything in between. However, one problem of floating point numbers is that they are normally represented with a limited amount of precision.

So you end up getting funny errors like \(0.1 + 0.2 = 0.30000000000000004\). This is problematic because the fractal viewer uses floating point math to do computations and so at some point, the error is too great and zooming into a fractal image any further results in distortions.

So how do we solve that? Well one way is by creating our own floating point number implementation so that we can use an arbitrary amount of precision to represent a number, allowing us to be more precise in our calculations. Now, the main challenge of doing so is accomplishing multiplications efficiently, and that led to creation of the following puzzle.

Setup

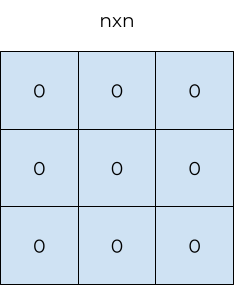
Assume you have an n by n grid, pictured below.

Goal

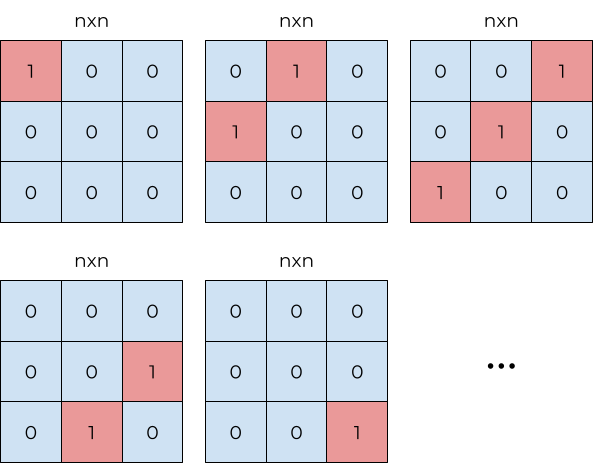
You want to find the smallest set of rectangles and squares required so that you can form any of the diagonals that slant up and to the right (as shown below).

Rules

Rules for creating shapes

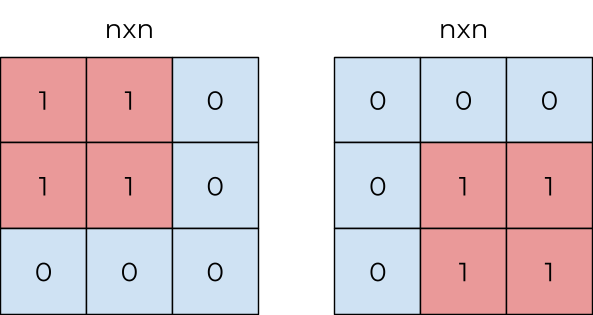
You can only create a square or a rectangle. They can be of any size. For the purposes of counting how many shapes we have, a shape in a different location is a completely new shape. For example, the image below shows two different squares.

Rules for combining rectangles and squares

Adding adds the values together, while subtracting subtracts the values as shown below.

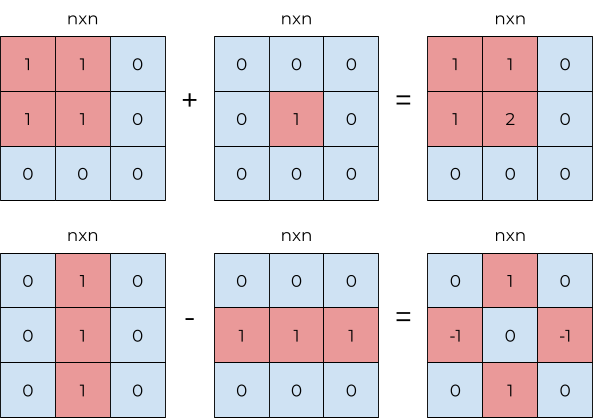
So we can think of this question in terms of set theory. That is, what is the smallest basis that allows us to create all of the up and to the right diagonals.

Applications

By now, you might be wondering why did you come up with something so esoteric as this? Why does this even matter and what is the motivation behind this toy problem?

So, the question came about when I was diving into the Karatsuba Multiplication Algorithm. I was creating a Fractal Viewer and was thinking of creating my own arbitrary precision arithmetic program for it. Obviously, this needed to be very efficient since I wouldn’t want to wait hours for the fractal images to render, and algorithms like Karatsuba’s would make my multiplication code more efficient.

Karatsuba Algorithm

So how does the algorithm work? Let’s first consider a regular multiplication. For example, if we want to compute \(34 \times 21\), we do \(30 \times 1 + 4 \times 1 + 30 \times 20 + 4 \times 20\). Notice how we have to do four multiplications here.

Another way to view the same operation is to use a table as shown in the figure below. The top-most row represents \(34\) and the left-most column represents \(21\). To do the multiplication, we do \(\text{row} \times \text{column}\).

Then, to read out the result of the multiplication, we add up all of the values of the diagonals starting from the bottom right corner and multiply it by \(10^{\text{diagonal index (zero-based index)}}\).

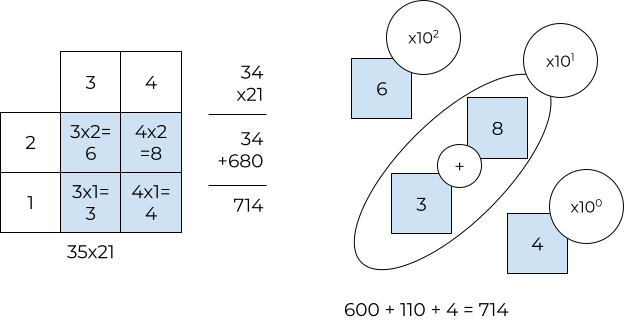
As you can see, to multiply \(34\) and \(21\), we had to do four multiplications. Multiplications are usually slower than addition, and so replacing them with addition and subtraction is often faster.

Karatsuba knew that and so they sought a way to avoid an extra multiplication. They noted that \((3 + 4) \times (2 + 1)\) is the same as doing \(6 + 8 + 3 + 4\). Their key insight is that if you only computed \((3 + 4) \times (2 + 1)\), \(3 \times 2\), and \(4 \times 1\), you can avoid computing \(4 \times 2\) and \(3 \times 1\) because \(\text{the middle diagonal} = 4 \times 2 + 3 \times 1 = (3 + 4) \times (2 + 1) - 3 \times 2 - 4 \times 1\).

So, to compute the diagonal values we only needed to compute:

1. \(3 \times 2\) to get 6
2. \((3 + 4) \times (2 + 1) - 3 \times 2 - 4 \times 1\) to get 3 + 8
3. And \(4 \times 1\) to get 4

This saves one multiplication because we reuse the result in steps 1 and 3 to compute step 2.

The Shape Analogy

So how does this connect to the shapes we mentioned at the beginning? Let’s define the value of a shape as \(\text{the sum of the column headers} \times \text{the sum of the row headers}\) for that specific square or rectangle. For example, refer to the below diagram.

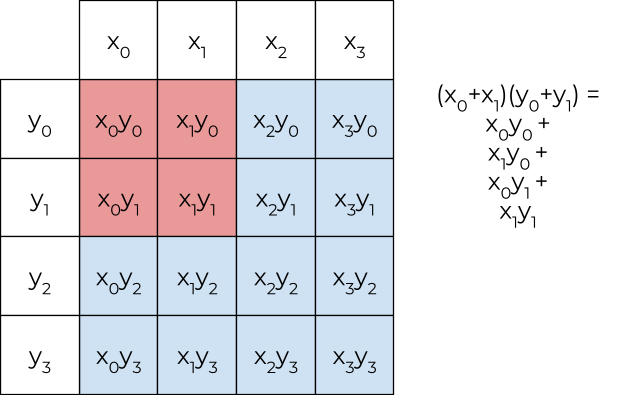
This definition is particularly convenient because each rectangle or square represents a single multiplication. Thus, by minimizing the number of rectangles or squares, we automatically minimize the number of multiplications. Adding or subtracting squares or rectangles corresponds to adding or subtracting the values of the squares or rectangles.

Once we add and subtract shapes to produce a diagonal shape using the rules described earlier, then the value of the diagonal shape represents a portion of the resulting product. For example, if it were the second diagonal shape from the bottom right corner, it would represent the value of the tenths place (with the exception of the carry value if it exists).

Karatsuba and the Shape Analogy

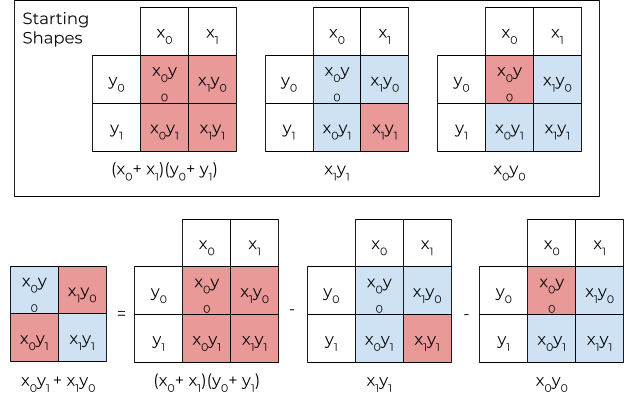
Now let’s look at Karatsuba’s approach using the shape analogy. Let’s consider multiplication but instead for arbitrary digits. So Karatsuba used three shapes. One was the entire square, and the other two were the top-left and the bottom-right corners.

From the start, the starting shapes include two of the required diagonals. The remaining diagonal shape can be recreated using a simple subtraction from the starting shapes. You can verify this fact using the corresponding math below each shape.

Purpose

Now my purpose in formulating this problem is to see if we can shift our perspective using the formulation above to find a generalized approach to Karatsuba’s multiplication method that is more efficient for larger sizes.

I am well aware of the work done by Toom and Cook, but frankly, it is not something I quite understand and requires some manipulations that are not as simple to implement as the Karatsuba algorithm.

My hope is that this new perspective might prove enlightening and that maybe some theorem from discrete mathematics, or some other field might apply here, and that maybe the shape formulation of the problem proves to be more tractable.

Further Reading

• Arithmetic Operations on Binary Numbers
• What Every Computer Scientist Should Know About Floating-Point Arithmetic
• Toom-Cook Algorithm for Multiplication
• Karatsuba Algorithm for Multiplication